Discriminant Analysis

Distance-based Discriminator

Given dataset of $N$ datapoints $\mathbf{X}=\{{\mathbf{x}}_i{\}}_{i=1}^N$ (where ${\mathbf{x}}_i\in {\mathbb{R}}^D$) and corresponding labels $\mathbf{y}=\{y_i{\}}_{i=1}^N$ (where each $y_i\in \{0,1,...,C-1\}$), we can extract some useful patterns among the datapoints and then essentially forget the dataset. This procedure is called learning and the models which learn useful parameters from the dataset are known as parametric models. For simplicity we can assume that there are only 2 classes $\{+,-\}$ ($+$ can be considered 1 and $-$ can be considered $0$ or $-1$).

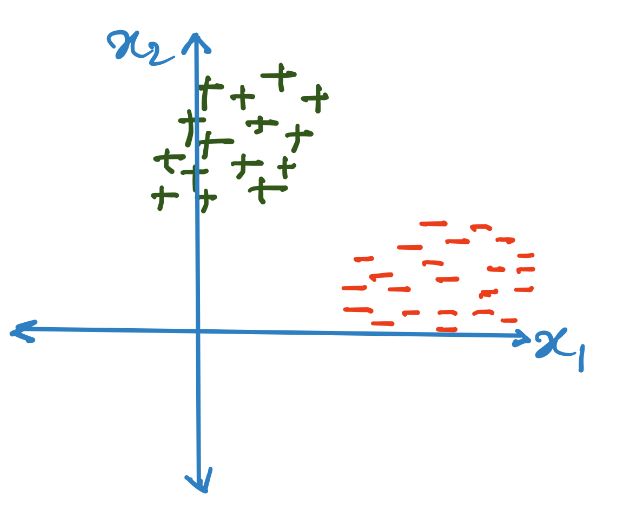
In the dataset described in the above image, we already know the labels. So, we can learn the means of the class conditional datapoints, i.e.

$${\mu }_j=\frac{1}{{\sum }_k{1}_{\{y_i=j\}}{\mathbf{x}}_k}\sum _i^N{1}_{\{y_k=j\}}{\mathbf{x}}_i$$

We can create a simple discriminator function by comparing the new datapoint with the class conditional means, with the label of the new datapoint being same as the most similar mean, i.e.

$$y_{new}=\arg \underset{j}{\max }⟨{\mu }_j,{\mathbf{x}}_{new}⟩$$

Fisher Discriminant Analysis

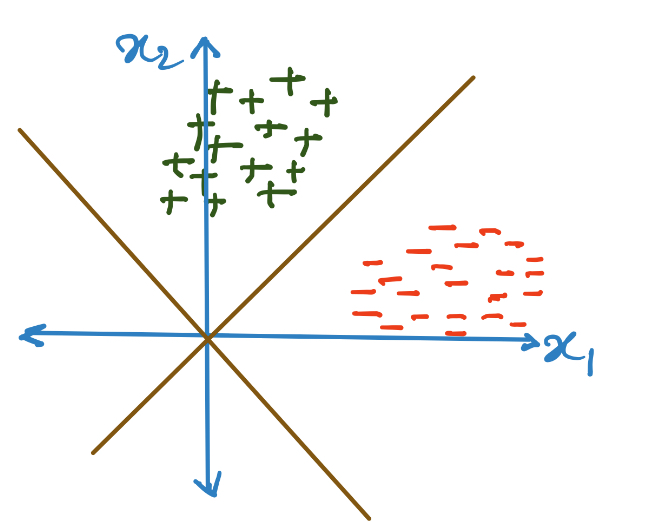
We can additionally assume the dataset to be sampled from a Gaussian. Fisher thought of trying to find a linear projection of the given dataset. This data can be projected on the standard basis or on other subspaces as shown below (linear projections):

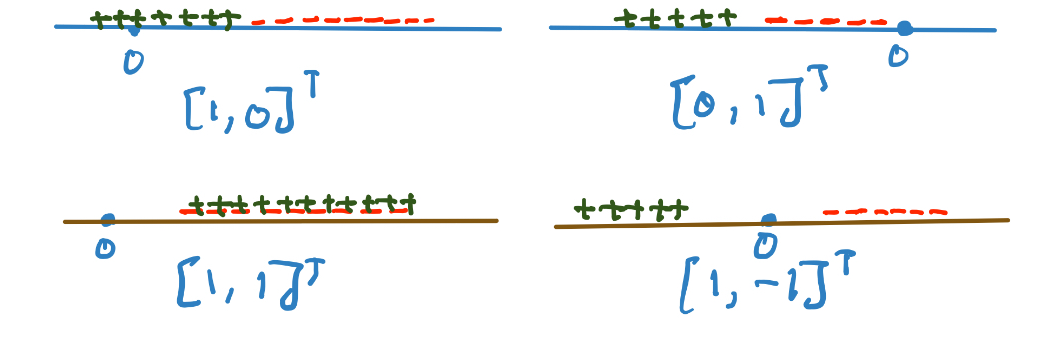
As we can see, not all choices for the linear projection are equally got at preserving the class information and giving a classifier which might generalize well.

We want to identify a vector for linear projection that

1. maximizes the between-class spread, and
2. minimizes the within-class spread.

Let the means after the linear projection be $m_1$ and $m_2$, and the variances be $s_1$ and $s_2$.

So, we would like to make the following ratio big:

$$R=\frac{(m_1-m_2{)}^2}{s_1^2+s_2^2}$$

We can assume that $m_1={\mathbf{w}}^T{\mu }_1$ and $m_2={\mathbf{w}}^T{\mu }_2$ where ${\mu }_1$ and ${\mu }_2$ are the actual means of the class conditional data distributions. Therefore:

$$m_1-m_2={\mathbf{w}}^T({\mu }_1-{\mu }_2)$$

Similarly $s_1^2+s_2^2$ can be written as:

$${\mathbf{w}}^T{\mathbf{S}}_1\mathbf{w}+{\mathbf{w}}^T{\mathbf{S}}_1\mathbf{w}={\mathbf{w}}^T\mathbf{Sw}$$

where $\mathbf{S}$ is the covariance matrix of the entire dataset.

Again,

$${\left({\mathbf{w}}^T({\mu }_1-{\mu }_2)\right)}^2={\mathbf{w}}^T({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T\mathbf{w}={\mathbf{w}}^T\mathbf{Mw}$$

Therefore, the objective is:

$$\underset{\mathbf{w}}{\max }R(\mathbf{w})=\frac{{\mathbf{w}}^T\mathbf{Mw}}{{\mathbf{w}}^T\mathbf{Sw}}$$

We can take the gradient:

$$\begin{array}{rl}{\nabla }_{\mathbf{w}}R(\mathbf{w})=({\mathbf{w}}^T\mathbf{Sw})\frac{\partial }{\partial \mathbf{w}}({\mathbf{w}}^T\mathbf{Mw})-({\mathbf{w}}^T\mathbf{Mw})\frac{\partial }{\partial \mathbf{w}}({\mathbf{w}}^T\mathbf{Sw})& =0\\ ⟹({\mathbf{w}}^T\mathbf{Sw})(2\mathbf{Mw})-({\mathbf{w}}^T\mathbf{Mw})(2\mathbf{Sw})& =0\\ ⟹\mathbf{Mw}& =\frac{{\mathbf{w}}^T\mathbf{Mw}}{{\mathbf{w}}^T\mathbf{Sw}}\mathbf{Sw}\\ ⟹\mathbf{Mw}& =R\mathbf{Sw}\\ ⟹\mathbf{Rw}& ={\mathbf{S}}^{-1}\mathbf{Mw}\\ ⟹\mathbf{Rw}& ={\mathbf{S}}^{-1}({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T\mathbf{w}\\ ⟹\mathbf{Rw}& =({\mu }_1-{\mu }_2{)}^T\mathbf{w}{\mathbf{S}}^{-1}({\mu }_1-{\mu }_2)\\ ⟹\mathbf{w}& =\frac{({\mu }_1-{\mu }_2{)}^T\mathbf{w}}{\mathbf{R}}{\mathbf{S}}^{-1}({\mu }_1-{\mu }_2)\\ ⟹\mathbf{w}& \propto {\mathbf{S}}^{-1}({\mu }_1-{\mu }_2)\end{array}$$

Thus, the projection surface is along the direction ${\mathbf{S}}^{-1}({\mu }_1-{\mu }_2)$.

---

Probabilistic view of Discriminant Analysis

We can learn a generative model and estimate the distribution that generated the dataset for each class separately, i.e. $\mathbb{P}({\mathbf{x}}_i|y_i=k)$. Given the generative model, we can use Bayes rule to design an optimal classifier.

Since we are in the binary classification domain ($y_i\in \{0,1\}$):

$$\mathbb{P}(y_i=1|{\mathbf{x}}_i)=\frac{\mathbb{P}({\mathbf{x}}_i|y_i=1)\mathbb{P}(y_i=1)}{\mathbb{P}({\mathbf{x}}_i|y_i=1)\mathbb{P}(y_i=1)+\mathbb{P}({\mathbf{x}}_i|y_i=0)\mathbb{P}(y_i=0)}$$

We can denote prior probabilities $\mathbb{P}(y_i=k)$ as ${\pi }_k$ where ${\pi }_1+{\pi }_0=1$ and ${\pi }_k$ can be estimated from the dataset as:

$${\pi }_k=\frac{1}{N}\sum _{i=1}^N{1}_{\{y_i=k\}}$$

Therefore:

$$\mathbb{P}(y_i=1|{\mathbf{x}}_i)=\frac{{\pi }_1\mathbb{P}({\mathbf{x}}_i|y_i=1)}{{\pi }_0\mathbb{P}({\mathbf{x}}_i|y_i=0)+{\pi }_1\mathbb{P}({\mathbf{x}}_i|y_i=1)}$$

In the context of Discriminant Analysis, we assume that the class conditional datapoints were sampled from Gaussian distributions. Since we are considering the binary classification problem, the parameters are $({\mu }_1,{\Sigma }_1)$ and $({\mu }_0,{\Sigma }_0)$ for the positive and negative class respectively.

Given a class label, it is easy to estimate the parameters Class conditional sample mean: ${\mu }_k=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{x}}_i$, and Class conditional sample covariance matrix: ${\Sigma }_k=\frac{1}{N-1}{\sum }_{i=1}^N({\mathbf{x}}_i-{\mu }_k)({\mathbf{x}}_i-{\mu }_k{)}^T$ Additionally, we already know the priors: ${\pi }_k=\frac{1}{N}{\sum }_{i=1}^N{1}_{\{y_i=k\}}$

Now all we need to do is find a decision rule. The decision boundary is given by the region where $\mathbb{P}(y_i=0|{\mathbf{x}}_i)=\mathbb{P}(y_i=1|{\mathbf{x}}_i)$.

Quadratic Discriminant Analysis

For a gaussian:

$$\begin{array}{rl}\mathbb{P}(y_i=0|{\mathbf{x}}_i)& =\mathbb{P}(y_i=1|{\mathbf{x}}_i)\\ ⟹\mathbb{P}({\mathbf{x}}_i|y_i=0){\pi }_0& =\mathbb{P}({\mathbf{x}}_i|y_i=1){\pi }_1\\ ⟹\log \mathbb{P}({\mathbf{x}}_i|y_i=0)+\log {\pi }_0& =\log \mathbb{P}({\mathbf{x}}_i|y_i=1)+\log {\pi }_1\\ ⟹\log \left((2\pi {)}^{-D/2}|{\Sigma }_0{|}^{-1/2}\exp \left(-0.5({\mathbf{x}}_i-{\mu }_0{)}^T{\Sigma }_0^{-1}({\mathbf{x}}_i-{\mu }_0)\right)\right)& +\log {\pi }_0=\\ \log \left((2\pi {)}^{-D/2}|{\Sigma }_1{|}^{-1/2}\exp \left(-0.5({\mathbf{x}}_i-{\mu }_1{)}^T{\Sigma }_1^{-1}({\mathbf{x}}_i-{\mu }_1)\right)\right)& +\log {\pi }_1\end{array}$$

Classification rule (for QDA): Let the ratio be

$$R=\frac{\log {\pi }_1-0.5\log |{\Sigma }_1|-0.5({\mathbf{x}}_i-{\mu }_1{)}^T{\Sigma }_1^{-1}({\mathbf{x}}_i-{\mu }_1)}{\log {\pi }_0-0.5\log |{\Sigma }_0|-0.5({\mathbf{x}}_i-{\mu }_0{)}^T{\Sigma }_0^{-1}({\mathbf{x}}_i-{\mu }_0)}$$

Then $y_i=1$ if $R>1$ else $y_i=0$.

Linear Discriminant Analysis

We can further assume that we have the same covariance matrix for both the classes, i.e. ${\Sigma }_0={\Sigma }_1=\Sigma$.

We can expand

$$\begin{array}{rl}({\mathbf{x}}_i-{\mu }_j{)}^T{\Sigma }^{-1}({\mathbf{x}}_i-{\mu }_j)& =({\mathbf{x}}_i-{\mu }_j{)}^T({\Sigma }^{-1}{\mathbf{x}}_i-{\Sigma }^{-1}{\mu }_j)\\ & ={\mathbf{x}}_i^T{\Sigma }^{-1}{\mathbf{x}}_i-2{\mathbf{x}}_i^T{\Sigma }^{-1}{\mu }_j+{\mu }_j^T{\Sigma }^{-1}{\mu }_j\end{array}$$

Therefore,

$$\begin{array}{rl}\log {\pi }_1+{\mathbf{x}}_i^T{\Sigma }^{-1}{\mu }_1-0.5{\mu }_1^T{\Sigma }^{-1}{\mu }_1& =\log {\pi }_0+{\mathbf{x}}_i^T{\Sigma }^{-1}{\mu }_0-0.5{\mu }_0^T{\Sigma }^{-1}{\mu }_0\\ ⟹{\mathbf{x}}_i^T{\Sigma }^{-1}{\mu }_0-{\mathbf{x}}_i^T{\Sigma }^{-1}{\mu }_1& =\log {\pi }_1-\log {\pi }_0+0.5{\mu }_0^T{\Sigma }^{-1}{\mu }_0-0.5{\mu }_1^T{\Sigma }^{-1}{\mu }_1\\ ⟹{\mathbf{x}}_i^T{\Sigma }^{-1}({\mu }_0-{\mu }_1)& =\log \frac{{\pi }_1}{{\pi }_0}+0.5({\mu }_0^T{\Sigma }^{-1}{\mu }_0-{\mu }_1^T{\Sigma }^{-1}{\mu }_1)=C\end{array}$$

where $C$ is a constant.

Notice that the term ${\mathbf{x}}_i^T{\Sigma }^{-1}({\mu }_0-{\mu }_1)$ is just the linear projection of ${\mathbf{x}}_i$ onto the direction ${\Sigma }^{-1}({\mu }_0-{\mu }_1)$, which is similar to Fisher Discriminant Analysis. Actually, LDA is exactly same as FDA, just derived from the probabilistic perspective.

Updated decision rule (for LDA): $y_i=1$ if ${\mathbf{x}}_i^T{\Sigma }^{-1}({\mu }_0-{\mu }_1)>C$ else $y_i=0$.